Cantor’s Theorem

P v. NP is a big problem in comptuer science. To learn more about it check this link out

Some background in Set Theory
In set theory, sets are basically arrays of any objects.
An example would be set alphabet = 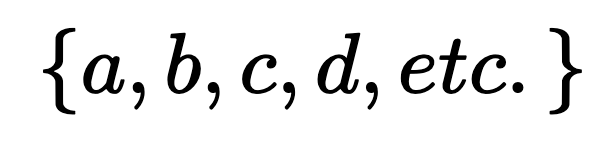The set can be anything from numbers to a list of fruits. Another concept in set theory is the powerset.
An easy way of thinking of powersets is the factors of a set. All the components that make it up but into smaller sets (subsets).

here’s an example of powersets: suppose we have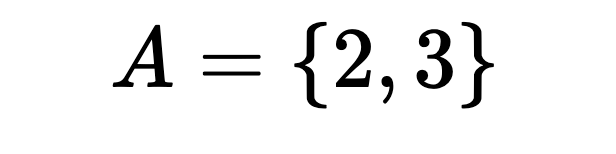

• means an empty set {}
  Another concept is Cardinality. It’s the number of elements in a set. So using the example of A: |A| = 2.
  ( “||” is the symbol for cardinality)
  So what would be the cardinality of a set like all natural numbers?
  There’s a special answer to this.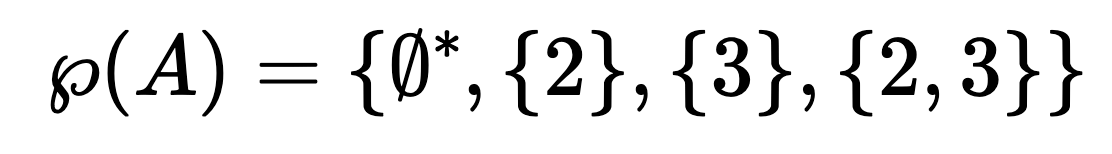 Because it’s the cardinal of an infinitly large set, that means that there’s infinite elements as well.

Pairing up set elements
When would a |Set A| = |Set B| ?
When we can match the elements of the set equally.
ex. Set A = {1, 2, 3} = Set B
Each element of the set has a counterpart in the other set, therefore their cardinalities are the same.
This is called one-to-one mapping or an bijection function formally. Each element of the powerset and the original set should be mapped onto each other.

Diagonal Proof
Cantor’s proof involved pairing up the sets 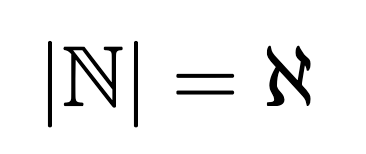but when he actually paired them up (injectively) he noticed a diagonal section of the sets which were never paired up. This continued on for the set length, proving that there’s an infinite number that can’t pair.
suppose 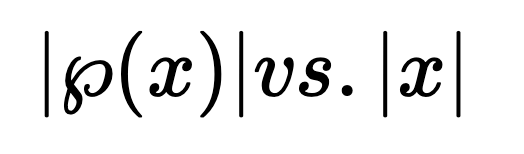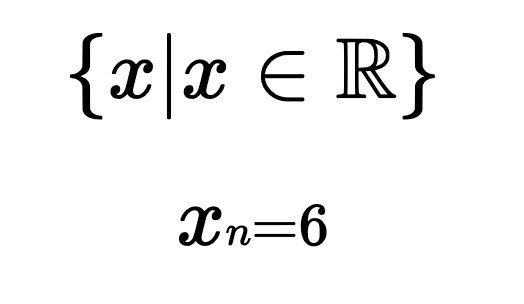and that via infinite decimal expansion that the nth element is 6. But because of the counterpart set the nth element has to also be seen as a function of the expansion f(n) such that the n element is 4 and f(n)=6.
Those numbers are arbitrary but for any n, f(n) won’t equal the x observed by the original set.
Therefore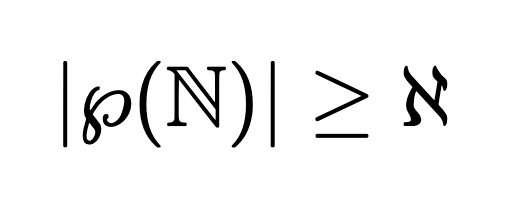

Application to Theory of Computation
This shows something important in the theory of computation though.
A string is a sequence of characters. So that means that there’s at least as many problems as the cardinality of all sets of strings.
Every computer program is a string, meaning that the number of programs is at most the number of strings. Cantor’s theorem implies that there’s more sets of strings than actual strings.
There are more problems than answers… You could pick a problem at random and the probability of solving it is ZERO.
There’s problems that computer’s can’t solve.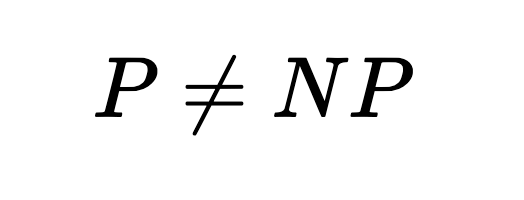

If you want to check out a more formal math-y proof check this out.